
Bitcoin uses ECDSA, or Elliptic Curve Digital Signature Algorithm, to produce private keys and public keys.
An elliptic curve is just a mathematical curve defined by the general form y^2 = x^3 + ax + b We take everything over a finite field because we want to encode every value possible in a constant amount of space.
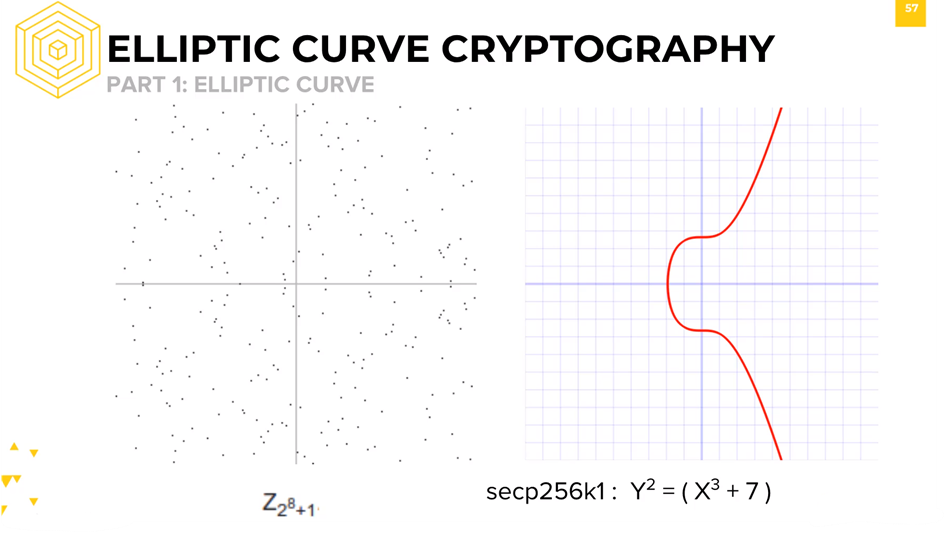
So here’s a picture of Bitcoin’s elliptic curve, secp256k1, on the right side.
It’s equation is y^2 = x^3 + 7, and was engineered to have some unique properties that we’ll be explaining in the coming slides.
As mentioned earlier, it’s taken over a finite field so as to limit key size.
To illustrate, on the left side is the same curve, but over a small field where we only have integer values -128 to 128.
When we take it over a finite field, it doesn’t look like a smooth curve anymore.
However, there are unique properties of elliptic curves that will help us in creating a one-way function to generate public keys from private keys.

So as mentioned earlier, Bitcoin’s elliptic curve is secp256k1.
This curve is specified with a couple parameters, including the actual curve formula itself (by its coefficients), the field, and a generator point.
Note the symmetry of the curve across the x axis.
This symmetry is preserved even when taking it over a finite field.
Also note that any non-vertical line on this curve will intersect the curve in at most 3 points.
On the graph on the right hand side, the line through points P and Q intersect at point R.
On this elliptic curve, we can do point addition using lines and points.
To add P plus Q, we can simply draw a line through them, intersecting at a third point R, and then reflect the point R across the x-axis , yielding our result P + Q.
And this is called the chord tangent process.
This is a trapdoor, or one-way, function, because given a point K that is P + Q, it is difficult to find the individual points P and Q.

